A subset 
of a topological space 
is compact
if for every open cover of 
, there exists a finite subcover of 
.
즉, S의 open cover들에 대해서, S의 finite subcover(element가 유한한 open cover of S의 subset)가 존재하는 경우, S가 compact하다고 한다.
cover
A family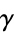 
of nonempty subsets of 
whose union contains the given set 
(and which contains no duplicated subsets) is called a cover (or covering) of 
For example of cover
there is only a single cover of 
,
namely 
.
However, there are five covers of 
,
namely 
, 
, 
, 
, and 
.
minimal cover
A minimal cover is a cover for which removal of one member destroys the covering property.
Open cover
A collection of open sets of a topological space whose union contains a given subset. Example of open cover
- an open cover of the real line, with respect to the Euclidean topology, is the set of all open intervals 
, where 
. - The set of all intervals 
, where 
, is an open cover of the open interval 
.
in a metric space 
is bounded if it has a finite generalized diameter, 
such that 
for all 
. 
is bounded iff it is contained inside some ball 
of finiteradius 
(Adams 1994).
